Note
Go to the end to download the full example code
Blended forecast#
This tutorial shows how to construct a blended forecast from an ensemble nowcast using the STEPS approach and a Numerical Weather Prediction (NWP) rainfall forecast. The used datasets are from the Bureau of Meteorology, Australia.
import os
from datetime import datetime
import numpy as np
from matplotlib import pyplot as plt
import pysteps
from pysteps import io, rcparams, blending
from pysteps.visualization import plot_precip_field
Read the radar images and the NWP forecast#
First, we import a sequence of 3 images of 10-minute radar composites and the corresponding NWP rainfall forecast that was available at that time.
You need the pysteps-data archive downloaded and the pystepsrc file configured with the data_source paths pointing to data folders. Additionally, the pysteps-nwp-importers plugin needs to be installed, see pySTEPS/pysteps-nwp-importers.
# Selected case
date_radar = datetime.strptime("202010310400", "%Y%m%d%H%M")
# The last NWP forecast was issued at 00:00
date_nwp = datetime.strptime("202010310000", "%Y%m%d%H%M")
radar_data_source = rcparams.data_sources["bom"]
nwp_data_source = rcparams.data_sources["bom_nwp"]
Load the data from the archive#
root_path = radar_data_source["root_path"]
path_fmt = "prcp-c10/66/%Y/%m/%d"
fn_pattern = "66_%Y%m%d_%H%M00.prcp-c10"
fn_ext = radar_data_source["fn_ext"]
importer_name = radar_data_source["importer"]
importer_kwargs = radar_data_source["importer_kwargs"]
timestep = 10.0
# Find the radar files in the archive
fns = io.find_by_date(
date_radar, root_path, path_fmt, fn_pattern, fn_ext, timestep, num_prev_files=2
)
# Read the radar composites
importer = io.get_method(importer_name, "importer")
radar_precip, _, radar_metadata = io.read_timeseries(fns, importer, **importer_kwargs)
# Import the NWP data
filename = os.path.join(
nwp_data_source["root_path"],
datetime.strftime(date_nwp, nwp_data_source["path_fmt"]),
datetime.strftime(date_nwp, nwp_data_source["fn_pattern"])
+ "."
+ nwp_data_source["fn_ext"],
)
nwp_importer = io.get_method("bom_nwp", "importer")
nwp_precip, _, nwp_metadata = nwp_importer(filename)
# Only keep the NWP forecasts from the last radar observation time (2020-10-31 04:00)
# onwards
nwp_precip = nwp_precip[24:43, :, :]
Rainfall values are accumulated. Disaggregating by time step
Pre-processing steps#
# Make sure the units are in mm/h
converter = pysteps.utils.get_method("mm/h")
radar_precip, radar_metadata = converter(radar_precip, radar_metadata)
nwp_precip, nwp_metadata = converter(nwp_precip, nwp_metadata)
# Threshold the data
radar_precip[radar_precip < 0.1] = 0.0
nwp_precip[nwp_precip < 0.1] = 0.0
# Plot the radar rainfall field and the first time step of the NWP forecast.
date_str = datetime.strftime(date_radar, "%Y-%m-%d %H:%M")
plt.figure(figsize=(10, 5))
plt.subplot(121)
plot_precip_field(
radar_precip[-1, :, :],
geodata=radar_metadata,
title=f"Radar observation at {date_str}",
colorscale="STEPS-NL",
)
plt.subplot(122)
plot_precip_field(
nwp_precip[0, :, :],
geodata=nwp_metadata,
title=f"NWP forecast at {date_str}",
colorscale="STEPS-NL",
)
plt.tight_layout()
plt.show()
# transform the data to dB
transformer = pysteps.utils.get_method("dB")
radar_precip, radar_metadata = transformer(radar_precip, radar_metadata, threshold=0.1)
nwp_precip, nwp_metadata = transformer(nwp_precip, nwp_metadata, threshold=0.1)
# r_nwp has to be four dimentional (n_models, time, y, x).
# If we only use one model:
if nwp_precip.ndim == 3:
nwp_precip = nwp_precip[None, :]
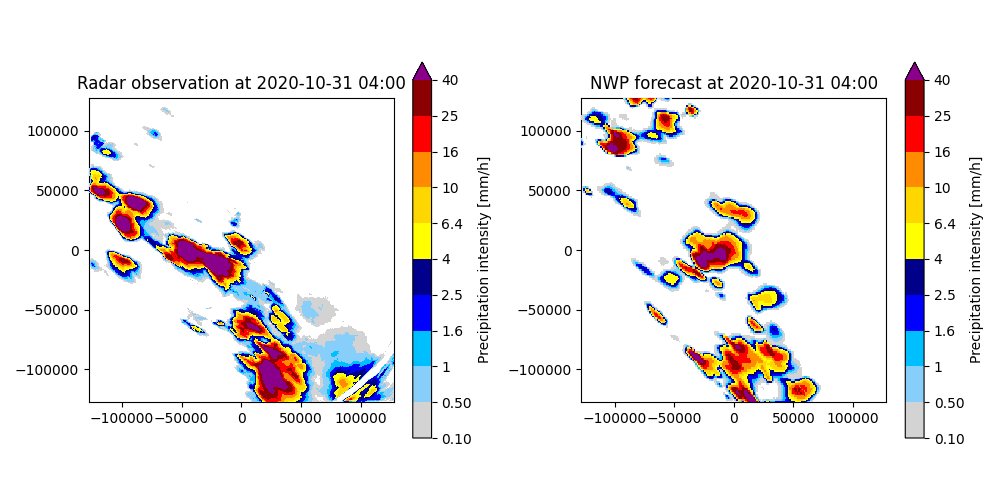
For the initial time step (t=0), the NWP rainfall forecast is not that different from the observed radar rainfall, but it misses some of the locations and shapes of the observed rainfall fields. Therefore, the NWP rainfall forecast will initially get a low weight in the blending process.
Determine the velocity fields#
oflow_method = pysteps.motion.get_method("lucaskanade")
# First for the radar images
velocity_radar = oflow_method(radar_precip)
# Then for the NWP forecast
velocity_nwp = []
# Loop through the models
for n_model in range(nwp_precip.shape[0]):
# Loop through the timesteps. We need two images to construct a motion
# field, so we can start from timestep 1. Timestep 0 will be the same
# as timestep 1.
_v_nwp_ = []
for t in range(1, nwp_precip.shape[1]):
v_nwp_ = oflow_method(nwp_precip[n_model, t - 1 : t + 1, :])
_v_nwp_.append(v_nwp_)
v_nwp_ = None
# Add the velocity field at time step 1 to time step 0.
_v_nwp_ = np.insert(_v_nwp_, 0, _v_nwp_[0], axis=0)
velocity_nwp.append(_v_nwp_)
velocity_nwp = np.stack(velocity_nwp)
The blended forecast#
precip_forecast = blending.steps.forecast(
precip=radar_precip,
precip_models=nwp_precip,
velocity=velocity_radar,
velocity_models=velocity_nwp,
timesteps=18,
timestep=timestep,
issuetime=date_radar,
n_ens_members=1,
precip_thr=radar_metadata["threshold"],
kmperpixel=radar_metadata["xpixelsize"] / 1000.0,
noise_stddev_adj="auto",
vel_pert_method=None,
)
# Transform the data back into mm/h
precip_forecast, _ = converter(precip_forecast, radar_metadata)
radar_precip, _ = converter(radar_precip, radar_metadata)
nwp_precip, _ = converter(nwp_precip, nwp_metadata)
STEPS blending
==============
Inputs
------
forecast issue time: 2020-10-31T04:00:00
input dimensions: 512x512
km/pixel: 0.5
time step: 10.0 minutes
NWP and blending inputs
-----------------------
number of (NWP) models: 1
blend (NWP) model members: False
decompose (NWP) models: yes
Methods
-------
extrapolation: semilagrangian
bandpass filter: gaussian
decomposition: fft
noise generator: nonparametric
noise adjustment: yes
velocity perturbator: None
blending weights method: bps
conditional statistics: no
precip. mask method: incremental
probability matching: cdf
FFT method: numpy
domain: spatial
Parameters
----------
number of time steps: 18
ensemble size: 1
parallel threads: 1
number of cascade levels: 8
order of the AR(p) model: 2
precip. intensity threshold: -10.0
no-rain fraction threshold for radar: 0.0
Field is below no rain fraction : False
rain fraction is : 0.22774505615234375
Field is below no rain fraction : False
rain fraction is : 0.22812230963456004
Computing noise adjustment coefficients... done.
noise std. dev. coeffs: [0.98357592 1.35448094 1.09212422 1.01751917 0.84585211 0.670512
0.57517317 0.53538232]
************************************************
* Correlation coefficients for cascade levels: *
************************************************
-----------------------------------------
| Level | Lag-1 | Lag-2 |
-----------------------------------------
| 1 | 0.996190 | 0.987414 |
-----------------------------------------
| 2 | 0.978659 | 0.927543 |
-----------------------------------------
| 3 | 0.905150 | 0.773399 |
-----------------------------------------
| 4 | 0.715544 | 0.481070 |
-----------------------------------------
| 5 | 0.387409 | 0.139512 |
-----------------------------------------
| 6 | 0.181822 | 0.097797 |
-----------------------------------------
| 7 | 0.152330 | 0.163940 |
-----------------------------------------
| 8 | 0.135901 | 0.152165 |
-----------------------------------------
****************************************
* AR(p) parameters for cascade levels: *
****************************************
------------------------------------------------------
| Level | Phi-1 | Phi-2 | Phi-0 |
------------------------------------------------------
| 1 | 1.648780 | -0.655085 | 0.065888 |
------------------------------------------------------
| 2 | 1.623665 | -0.659072 | 0.154547 |
------------------------------------------------------
| 3 | 1.135050 | -0.253991 | 0.411152 |
------------------------------------------------------
| 4 | 0.760900 | -0.063388 | 0.697163 |
------------------------------------------------------
| 5 | 0.392228 | -0.012440 | 0.921837 |
------------------------------------------------------
| 6 | 0.169648 | 0.066952 | 0.981125 |
------------------------------------------------------
| 7 | 0.130382 | 0.144079 | 0.978018 |
------------------------------------------------------
| 8 | 0.117389 | 0.136212 | 0.981489 |
------------------------------------------------------
Starting blended nowcast computation.
Computing nowcast for time step 1... done.
Computing nowcast for time step 2... done.
Computing nowcast for time step 3... done.
Computing nowcast for time step 4... done.
Computing nowcast for time step 5... done.
Computing nowcast for time step 6... done.
Computing nowcast for time step 7... done.
Computing nowcast for time step 8... done.
Computing nowcast for time step 9... done.
Computing nowcast for time step 10... done.
Computing nowcast for time step 11... done.
Computing nowcast for time step 12... done.
Computing nowcast for time step 13... done.
Computing nowcast for time step 14... done.
Computing nowcast for time step 15... done.
Computing nowcast for time step 16... done.
Computing nowcast for time step 17... done.
Computing nowcast for time step 18... done.
Visualize the output#
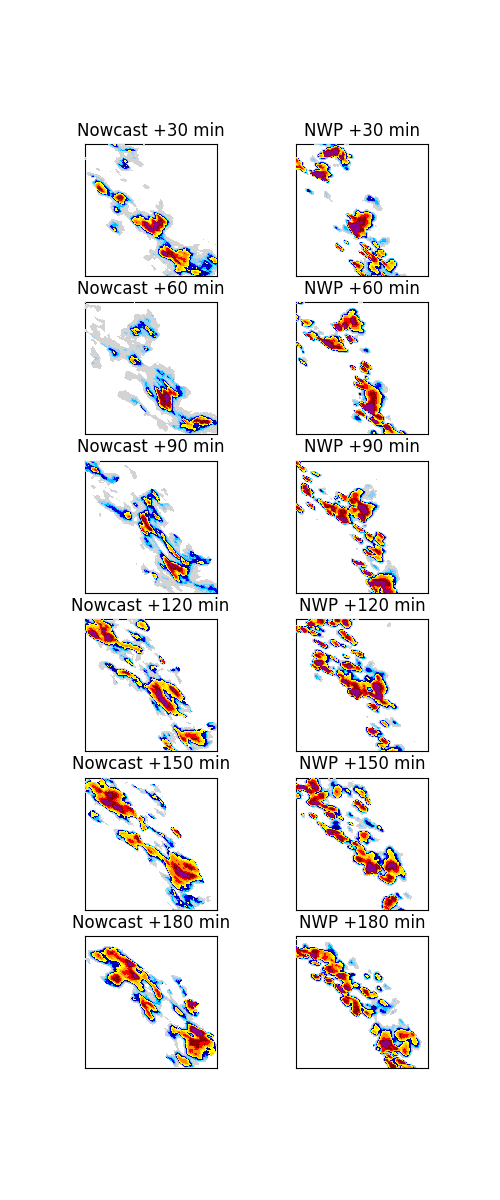
The NWP rainfall forecast has a lower weight than the radar-based extrapolation forecast at the issue time of the forecast (+0 min). Therefore, the first time steps consist mostly of the extrapolation. However, near the end of the forecast (+180 min), the NWP share in the blended forecast has become more important and the forecast starts to resemble the NWP forecast more.
fig = plt.figure(figsize=(5, 12))
leadtimes_min = [30, 60, 90, 120, 150, 180]
n_leadtimes = len(leadtimes_min)
for n, leadtime in enumerate(leadtimes_min):
# Nowcast with blending into NWP
plt.subplot(n_leadtimes, 2, n * 2 + 1)
plot_precip_field(
precip_forecast[0, int(leadtime / timestep) - 1, :, :],
geodata=radar_metadata,
title=f"Nowcast +{leadtime} min",
axis="off",
colorscale="STEPS-NL",
colorbar=False,
)
# Raw NWP forecast
plt.subplot(n_leadtimes, 2, n * 2 + 2)
plot_precip_field(
nwp_precip[0, int(leadtime / timestep) - 1, :, :],
geodata=nwp_metadata,
title=f"NWP +{leadtime} min",
axis="off",
colorscale="STEPS-NL",
colorbar=False,
)
References#
Bowler, N. E., and C. E. Pierce, and A. W. Seed. 2004. “STEPS: A probabilistic precipitation forecasting scheme which merges an extrapolation nowcast with downscaled NWP.” Forecasting Research Technical Report No. 433. Wallingford, UK.
Bowler, N. E., and C. E. Pierce, and A. W. Seed. 2006. “STEPS: A probabilistic precipitation forecasting scheme which merges an extrapolation nowcast with downscaled NWP.” Quarterly Journal of the Royal Meteorological Society 132(16): 2127-2155. https://doi.org/10.1256/qj.04.100
Seed, A. W., and C. E. Pierce, and K. Norman. 2013. “Formulation and evaluation of a scale decomposition-based stochastic precipitation nowcast scheme.” Water Resources Research 49(10): 6624-664. https://doi.org/10.1002/wrcr.20536
Total running time of the script: (1 minutes 3.005 seconds)
